前言
Decision-making Trial and Evaluation Laboratory(DEMATEL)直译为决策实验室分析。DEMATEL也有翻译成决策与试验评价实验室,或者简称实验室法。DEMATEL为首字母缩写,一般情况下,念[de mei tel] 或者念 [di mie tel]。1971年在日内瓦的一次会议上美国Battelle实验室的学者A. Gabus和E. Fontela提出的为了解现实世界中复杂、困难的问题而提出的方法论,是一种运用图论和矩阵工具的系统分析的方法。
DEMATEL方法种类
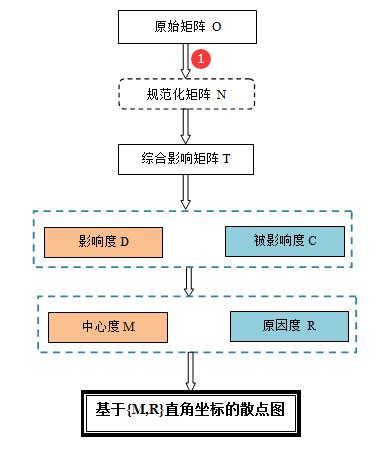
一个输入即$O$
直接影响矩阵O为输入,即如果其它参数默认一致,最终的结果为自动运算生成。
一个参数设置,即规范化方法的设置
规范化方法(归一化)方法非常重要。通常采用的是行和最大值法。
输出结果为散点图
结果是散点图,是以中心度M为横轴,原因度R为纵轴。
常规DEMATEL计算
第一、交代原始数据的来源,即直接影响矩阵$O$(是一个人拍脑袋得来的吗?还是多人拍脑袋得来的)
第二、归一化的方法,即规范化的方法,得到归一化矩阵$N$,理解主对角线为什么全部为0
第三、综合影响矩阵$T$,理解主对角线为什么大部分为小数
第四、影响度与被影响度的求解(这步小学生一年级都会)
第五、原因度与中心度的求解(这步小学生一年级都会)
第六、散点图的绘制,如果非散点图,注意连线的合理性与连线的意义,别瞎搞。
DEMATEL-对比(比较)型的方式
第一、交代原始数据的来源,即直接影响矩阵$O$(是一个人拍脑袋得来的吗?还是多人拍脑袋得来的)
第二、归一化的方法,是一个参数设置,不同的归一化方法得到不同的规范化矩阵$N$,这意味着同一个原始数据采用同一个方法得到的结果不同。那么这个结果有什么特征,有什么不变的?
第三、该方法目前还未见人使用或者讨论,拓扑不变性是最基本的概念
FUZZY——DEMATEL,Grey——DEMATEL的对比型方式处理
FUZZY即模糊,可以简写成F-DEMATEL;Grey即灰色。
直接影响矩阵$O$的特点为存在最大值与最小值两种情况。
即可以用同一种规范化方法,获得最大值条件下的归一化矩阵,以及最小值条件下的归一化矩阵。
最终讨论原因度与中心度的排序变化情况
该方法目前还未见人使用或者讨论,拓扑不变性是最基本的概念
清晰化公式:$ s_{ij}= \frac{v_{ij}Max(u_{j})- (v_{ij})^2+( u_{ij})^2} {Max(u_{j})-v_{ij} + u_{ij}}$
DEMATEL-ISM联用方法
顾名思义,两者联用是DEMATEL方法在前,ISM方法在后。两者方法联用主要有两种方式:
第一、基于综合影响矩阵$T$的联用方式。即因果(影响与被影响)关系的层级划分。
第二、基于中心度$M$原因度$R$的优劣(重要性)比较关系的层级划分。
基于综合影响矩阵$T$的DEMATEL-ISM方法
处理流程图如下:
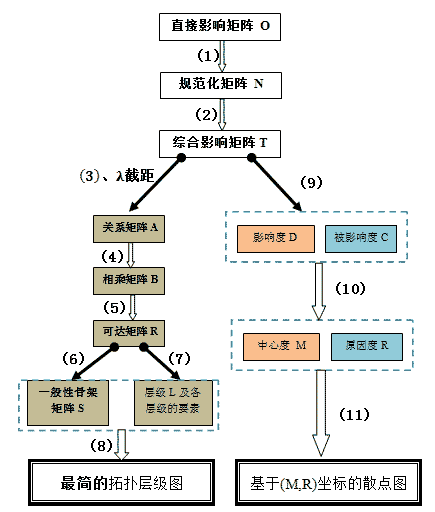
上述流程分为3个部分
$$ \require{cancel} \require{AMScd} \begin{CD} O @>>>N@>>>T \end{CD} $$
$$ \require{cancel} \require{AMScd} \begin{CD} T@>(3)>>A@>>>B@>>>R@>>>最简拓扑层级图 \end{CD} $$
$$ \require{cancel} \require{AMScd} \begin{CD} T@>>>\{D|C \}@>>>\{M|R \}@>>>以中心度M为横坐标、原因度R为纵坐标的构成的散点图 \end{CD} $$
一个输入
直接影响矩阵为输入,即如果其它参数默认一致,最终的结果为自动运算生成。
两个参数设置
第一、规范化方法,通常采用的是行和最大值法。
第二、截距λ取值的理由
两个输出结果
第一、最简的拓扑层级图,即一般性骨架矩阵的拓扑层次图
第二、直角坐标系的散点图,通常是以中心度M为横轴,原因度R为纵轴。
基于综合影响矩阵$T$全体截距$ \lambda $ 的DEMATEL-FISM联用。
第一、截距与截距阵模糊矩阵到布尔矩阵的转化。
模糊矩阵$\tilde F =( \tilde f_{ij})_{n \times n} $ 其取$\lambda$ 截距后,得截距阵记$F_{\lambda}=(f_{ij})_{n \times n}$
模糊矩阵$\tilde F $ 特征为矩阵值 $\tilde f_{ij}$为一小数形式。
截距阵$F_{\lambda}=(f_{ij})_{n \times n}$为布尔矩阵,其值为0或者1
截距阵转化:$ f _{ij}= \left\{ \begin{array}{ll} 1 & \textrm{当:$ \tilde f_{ij} > \lambda $}\\ 0 & \textrm{当:$ \tilde f_{ij} ≤ \lambda $ } \end{array} \right. $
第二、截矩阵的可达矩阵等价求法。
$\require{cancel} \require{AMScd} \begin{CD} \tilde B=\left[ \tilde b_{ij} \right]_{n \times n}@>最大最小算子>> \tilde R=\left[ \tilde r_{ij} \right]_{n \times n}@>截距>>R_{\lambda}=\left[ r_{ij} \right]_{n \times n} \\ \end{CD}$ 其中$\tilde R$为模糊可达矩阵
$ \begin{CD} \tilde B=\left[ \tilde b_{ij} \right]_{n \times n}@>截距>> \tilde B_{\lambda}=\left[ \tilde b_{ij} \right]_{n \times n}@>布尔可达矩阵求解>>R_{\lambda}=\left[ r_{ij} \right]_{n \times n} \\ \end{CD}$ 其中$\tilde B_{\lambda}$为模糊相乘矩阵的截距阵
上述两个方法是等价的,通常用先求模糊可达矩阵的方法,即第一种方法。
第三、从综合影响矩阵$T$求对应的层级拓扑图是一对多的关系。
$ \begin{CD} T=\left[ t_{ij} \right]_{n \times n}@>I+T>>\tilde B@>模糊可达矩阵求解>>\tilde R@>由阈值集合得截距阵>> \left\{ \begin{array}{} \\ \textrm{截距= $\lambda1$} & R_{\lambda1} @> ISM运算 >> 对应的层级拓扑图 \\ \\ \textrm{截距= $\lambda2$} & R_{\lambda2} @> ISM运算 >> 对应的层级拓扑图 \\ \\ \vdots & \vdots \\ \\ \textrm{截距= $\lambda n$} & R_{\lambda n} @> ISM运算 >> 对应的层级拓扑图 \\ \end{array} \right. \end{CD} $
第四、模糊相乘矩阵$\tilde B$ 的主对角线的值全部为1而不是大于1因为这是模糊数相加
第五、由于结果是一对多,且拓扑层级图的种类很多,给出所有的拓扑层次图意义不大,一般选取一个或者若干个来表示一下,对于大论文而言,这是灌水的好机会。
第六、随着截距的增加,拓扑层次图从一坨的大回路逐渐的变成了全部离散的点。
基于综合影响矩阵$T$全体截距$ \lambda $ 的DEMATEL-UISM联用。
第一、从综合影响矩阵$T$求不确定性解释结构模型,专门针对的是特定的截距,进行不确定解释结构模型运算。
$ \begin{CD} T=\left[ t_{ij} \right]_{n \times n}@>I+T>>\tilde B@>模糊可达矩阵求解>>\tilde R@>由阈值集合得截距阵>> \left\{ \begin{array}{} \\ \textrm{截距= $\lambda1$} & R_{\lambda1} @> UISM运算 >> 2^x个子结构 @> 去重 >> y个异构体 \\ \\ \textrm{截距= $\lambda2$} & R_{\lambda2} @> UISM运算 >> 2^x个子结构 @> 去重 >> y个异构体 \\ \\ \vdots & \vdots \\ \\ \textrm{截距= $\lambda n$} & R_{\lambda n} @> UISM运算 >> 2^x个子结构 @> 去重 >> y个异构体 \\ \end{array} \right. \end{CD} $
第二、当所取的截距的数值在模糊矩阵中的值存在多个才有意义
基于综合影响矩阵$T$统计学平均值特点的区段截距$\lambda $DEMATEL-WAISM联用。
第一、平均数,即综合影响矩阵$T$矩阵的均值$ \bar{x} $
第二、总体标准差$ \sigma $
$\sigma=\sqrt { \frac {\sum \limits_{i=1}^{n^2} ({x_i-\bar{x}})^2 }{n^2} } $
第三、区段截取的特征边界$ [\lambda_{min},\lambda_{max} ]$
$\lambda_{min}= \bar{x} $
$\lambda_{max}= \bar{x} +\sigma $
第四、流程
$ \begin{CD} T=\left[t_{ij} \right]_{n \times n}@>[\lambda_{min},\lambda_{max} ]截取>> \tilde A @> \tilde A+I>>\tilde B@>模糊可达矩阵求解>>\tilde R@>由阈值集合得截距阵>> \left\{ \begin{array}{} \\ \textrm{截距= $\lambda1$} & R_{\lambda1} @> ISM运算 >> 对应的层级拓扑图 \\ \\ \textrm{截距= $\lambda2$} & R_{\lambda2} @> ISM运算 >> 对应的层级拓扑图 \\ \\ \vdots & \vdots \\ \\ \textrm{截距= $\lambda n$} & R_{\lambda n} @> ISM运算 >> 对应的层级拓扑图 \\ \end{array} \right. \end{CD} $
第五、区段截取中,模糊矩阵的转化。$ T=\left[t_{ij} \right]_{n \times n} , \tilde A =\left[ \tilde a_{ij} \right]_{n \times n}$
$ \tilde a_{ij}= \begin{cases} 1 , \text{ $e_i$}\rightarrow \text{$e_j$ 当: $ t_{ij} > \lambda_{max} $} \\ t_{ij} , \text{ $e_i$}\rightarrow \text{$e_j $ 当:$\lambda_{min} ≤ t_{ij} ≤ \lambda_{max}$ } \\ 0, \text{ $e_i$}\rightarrow \text{$e_j$ 当: $ t_{ij} < \lambda_{min} $} \end{cases} $
$\lambda= \bar{x} + \sigma $ 硬算方式的DEMATEL-WAISM联用。
第一、平均数,即综合影响矩阵$T$矩阵的均值$ \bar{x} $
第二、总体标准差$ \sigma $
$\sigma=\sqrt { \frac {\sum \limits_{i=1}^{n^2} ({x_i-\bar{x}})^2 }{n^2} } $
第三、$ \lambda= \bar{x} + \sigma $
第四、流程
$ \begin{CD} T=\left[t_{ij} \right]_{n \times n}@>\lambda 截距>> A @> A+I>> B@>幂乘>>R@>结果优先>原因优先>(UP型层级|DOWN型层级)@> 代入WS>>(UP型图|DOWN型图) \end{CD} $
第五、截取中,模糊矩阵的转化。$ T=\left[t_{ij} \right]_{n \times n} , A =\left[ a_{ij} \right]_{n \times n}$
$ a_{ij}= \begin{cases} 1 , \text{ $e_i$}\rightarrow \text{$e_j$ 当: $ t_{ij} ≥ \lambda $} \\ 0, \text{ $e_i$}\rightarrow \text{$e_j$ 当: $ t_{ij} < \lambda $} \end{cases} $
第六、含综合影响值的一般性骨架矩阵$WS$计算过程
$\begin{CD} R @>缩点>>R' @>缩边>>S' @>增点>>S@>代入T中对应的值>>TS@>回路内部的有向边进行标注>>WS \\ \end{CD} \\$
基于{中心度M,原因度R}比较关系的DEMATEL-ISM方法
核心流程图
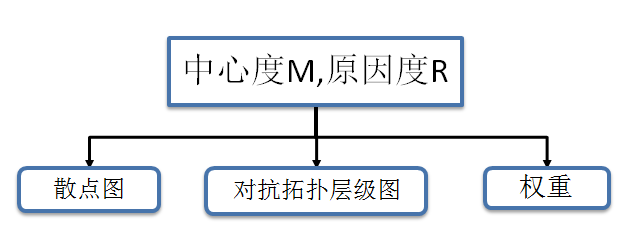
偏序-序拓扑概念
$$\begin{CD} D=\left[ d_{ij} \right]_{n \times m}@>偏序规则>>A=\left[a_{ij} \right]_{n \times n} \\\end{CD} $$
其中 $D=\left[ d_{ij} \right]_{n \times m}$ 为决策评价矩阵。$n$行$m$列。$n$代表评价对象(要素、方案、样本);$m$代表维度(准则、属性、目标)。
其中 $A=\left[ a_{ij} \right]_{n \times n}$ 为关系矩阵。是一个布尔方阵。$n$代表评价对象(要素、方案、样本)。
对于决策矩阵$D$中 $n$个要素的任何一列都具有严格的可比性。
偏序规则
对于含有m列的评价矩阵D,其中的任意一列即指标维度,具有同属性,可比较的前提。维度的这种优劣的比较至少有着两种属性。
数值越大越优,数值越小越差,称之为正向指标。记作p1、p2……pm。 数值越小越好,数值越大越差,称之为负向指标。记作q1、q2……qm。
对于决策矩阵$D$中的任意两行$x,y$
负向指标有 $d_{(x,p1)} \geqslant d_{(y,p1)} 且d_{(x,p2)} \geqslant d_{(y,p2)} 且 {\cdots}且d_{(x,pm)} \geqslant d_{(y,pm)}$ 同时有
正向指标有 $d_{(x,q1)} \leqslant d_{(y,q1)} 且d_{(x,q2)} \leqslant d_{(y,q2)} 且 {\cdots}且d_{(x,qm)} \leqslant d_{(y,qm)}$
符合上述规则,要素$x$与要素$y$的偏序关系记作:$x ≺ y$
$x \prec y$的意义为$y要素$优于(好于,牛逼于,帅于,猛于)$x要素$ 。
上述规则成为偏序规则。对于决策矩阵通过偏序规则可以得到关系矩阵 $A$
$$a_{xy}= \begin{cases} 1, x \prec y \\ 0, 其它 \end{cases} $$
取偏序的简单示例
把只有1列的决策矩阵$D$中的负向指标想象成排名,A1为第1名。关系矩阵$A$中 A2->A1即A2行A1列对应的单元格意思为A1比A2牛逼,即$A2 \prec A1$
$$ 示例二: \begin{CD} D=\begin{array}{c|c|c|c|c|c|c}{M_{17 \times2}} & 正向指标 & 正向指标 \\ \hline A1 &1.9223 &0.59336 \\ \hline A2 &2.86838 &0.16965\\ \hline A3 &1.38284 &0.22882\\ \hline \end{array} @>取偏序>> A=\begin{array}{c|c|c|c|c|c|c}{M_{3 \times 3}} & A1 &A2 &A3\\ \hline A1 &- & & \\ \hline A2 & &- &\\ \hline A3 &1 & & -\\ \hline \end{array} \end{CD} $$在三组数据中只有A3的两个属性值都小于于A1。关系矩阵$A$中 A3->A1即A3行A1列对应的单元格意思为A1比A3牛逼,即$A3 \prec A1$
重要性与夹逼的概念
核心流程图
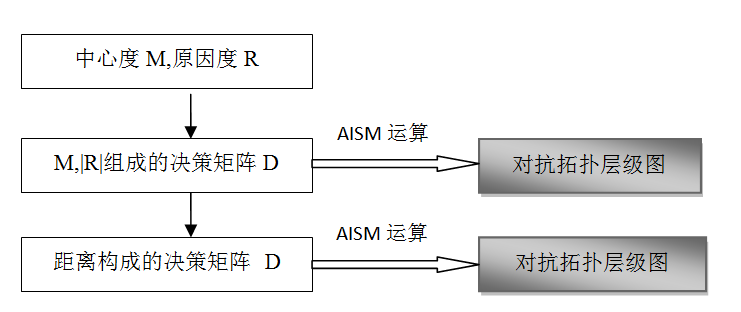
重要性
在DEMATEL方法中,M,R是评价要素重要性的内容,中心度的数值越高表示越越重要;原因度为负数时候代表为结果度,通常用绝对值来表示其重要性。
在评价体系中,通常把若干维度,最终运用欧式距离公式,以距离的形式表示其重要程度,距离越大越重要。
夹逼
纵向是夹逼的过程,即降维的过程。
$$ \begin{CD} D=\begin{array}{c|c|c|c|c|c|c}{M_{n \times2}} & 中心度M & 原因度绝对值 |R| \\ \hline E1 & M1 & |R1| \\ \hline \vdots & \vdots &\vdots\\ \hline E_n &M_n & |R_n|\\ \hline \end{array} @>夹逼、降维>> D=\begin{array}{c|c|c|c|c|c|c}{M_{n \times 1}} & 距离 d \\ \hline E1 & d1 \\ \hline \vdots & \vdots \\ \hline E_n & d_n \\ \hline \end{array} \end{CD} $$AISM流程
DEMATEL-ANP求权重
DEMATEL-ANP求权重的流程